Deep Into: linear regression and gradient descent

Hi, I'm ashen. I'm an undergraduate student at the Sabaragamuwa University of Sri Lanka, Department of Computing and Information System, faculty of applied sciences and this is my very first blog post. I hope to write a series of articles about machine learning algorithms and math behind the black-box. so this is the first one, and it's all about simple but powerful and super use full linear regression. also, I'll explain one of the optimization technique `gradient decent`. let's begin to dig!!!

what is linear regression?

simply, linear regression is a linear modelling technique for exploring the relationship between the scalar response variable and one or more explanatory variables. The first equation is the simple version of linear regression, and it only has one independent variable(feature) and one dependent variable(target/predictor). The second equation is a modified version of the first one. it contains multiple independent variables and one dependent variable. also, there is another version of this, which is multivariate, it has multiple independent and dependent variables and I’ve not covered it here. let's see this with real data set, I use the housing dataset from Kaggle. we try to predict house price with "overallqual, grlivarea, garagecars, garagearea, totalbsmtsf".

to make predictions we need to know the correlation and intercept of the linear model. to find them we use the ordinary least square method. it's something like this,

how this comes to here, let's see: we can imagine this dataset as a bunch of linear equations. like this,

in here X_ij are data points(under overallqual, grlivarea, garagecars, garagearea, totalbsmtsf features) in this data set, y_i1 are target feature(saleprice), β values are coefficent for each feature and c is the intercept. now we can display this as matrix equation Y = AX,

from this we can get:

so now we can implement this using python and find coefficent and intercept.

now we can use this class to training and get beta values.

this is our predictions on saleprice and predictions made 0.79 score.

predictions vs real values

so, what is gradient decent, when we use it?, let's see.

gradient decent

gradient descent is an iterative optimization technique to find optimal values for coefficent and intercept. we use partial derivation to find the gradient of cost function and rapidly reduce the cost to its minimum value. I reduce this dataset to one feature and target for demonstration purpose and then use whole dataset as before.

this is how ordinary least square method work in here with one feature.

this is our cost function:

if we get partial deravative by β then we have a gradient of the curve.

now I going to implement this in python. before that, we need to familiar with few terms used in machine learning, Hyper-parameter, epochs. hyper-parameter is a way to control complexity, behaviour or learning rate. Here’s the learning rate. epoch is the number of iterations we want to do in learning process.

in this figure, green marks show when using a large learning rate, and yellow marks show a small learning rate. when using a large learning rate it misses minimum cost and if its too small it takes a long time to complete the training process. So we have to choose the best learning rate to get optimal performance form gradient decent. if we choose a small learning rate with small epochs algorithm can't go all the way down in the cost curve. as I illustrate with yellow marks small learning rates need large epochs.

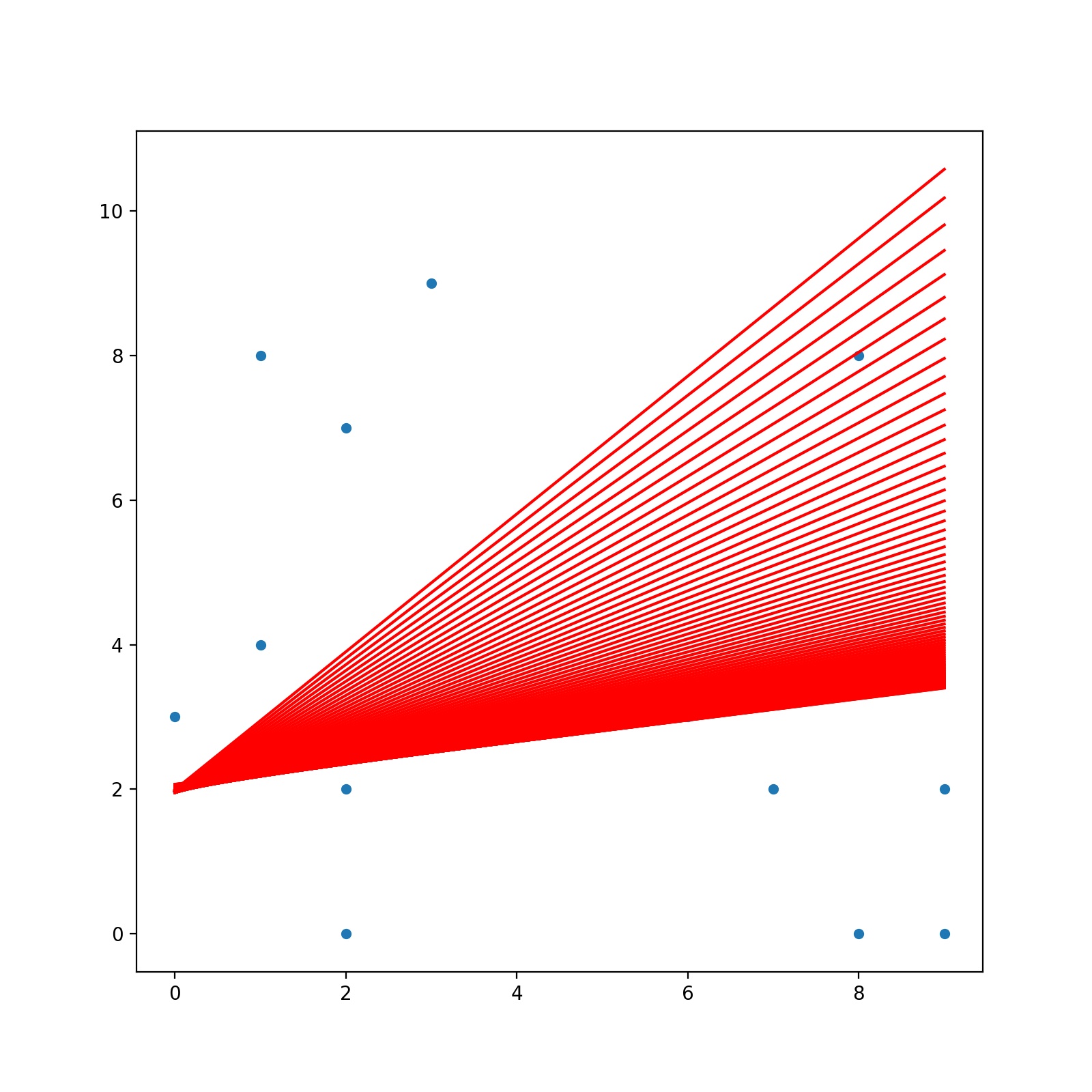
in the above graph I plotted 1000 lines through the training with updating β values. with this graph, we can get a clear idea about gradient descent. the red line is the final line. I plot blue lines with low opacity to show how it’s changed occurs through the learning process. I started by given 0 values to β and intercepts. when the learning process progress line change its coefficent and intercept and this how it’s looking through the learning process. as a final thought, gradient descent simply applies various coefficent values and intercepts to reduce cost and get optimal values for coefficent and intercept. so we reach to end of this article but this is not the end of this series. I’ll come with another algorithm soon. till then good luck!!